二叉树
- 二叉树的遍历方式
- 深度优先遍历:
- 前序遍历(递归法、迭代法): 中左右
- 中序遍历(递归法、迭代法): 左中右
- 后序遍历(递归法、迭代法): 左右中
- 广度优先遍历:
- 层序遍历(迭代法)
- 二叉树的定义
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x):val(x),left(nullptr),right(nullptr){}
};
二叉树的递归遍历
- 递归三部曲:
- 确定函数的参数和返回值;
- 确定终止条件;
- 确定单层递归的逻辑;
144. 二叉树的前序遍历
class Solution {
public:
void dfs(TreeNode* root,vector<int>& ret){// 参数&返回值
if(root == nullptr)return ;// 终止条件
ret.push_back(root->val);// 中
dfs(root->left,ret);// 左
dfs(root->right,ret);// 右
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int>ret;
dfs(root,ret);
return ret;
}
};
145. 二叉树的后序遍历
class Solution {
public:
void dfs(TreeNode* root,vector<int>& ret){// 参数&返回值
if(root == nullptr)return ;// 终止条件
dfs(root->left,ret);// 左
dfs(root->right,ret);// 右
ret.push_back(root->val);// 中
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int>ret;
dfs(root,ret);
return ret;
}
};
94. 二叉树的中序遍历
class Solution {
public:
void dfs(TreeNode* root,vector<int>& ret){// 参数&返回值
if(root == nullptr)return ;// 终止条件
dfs(root->left,ret);// 左
ret.push_back(root->val);// 中
dfs(root->right,ret);// 右
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int>ret;
dfs(root,ret);
return ret;
}
};
二叉树的迭代遍历
- 递归的实现就是:每一次递归调用都会
把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归为什么可以返回上一层位置的原因。- 所以我们知道,可以用
栈来实现二叉树的遍历。
144. 二叉树的前序遍历
// 中左右
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int>ret;
if(root == nullptr)return ret;
stack<TreeNode*>st;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
st.pop();
ret.push_back(node->val);
if(node->right)st.push(node->right);// 栈,所以先放左结点,先取出来的也是左结点
if(node->left)st.push(node->left);
}
return ret;
}
};
145. 二叉树的后序遍历
- 在中序遍历的迭代方法上,更改while内Push left/right的顺序,改成中右左,最后进行反转结果集即可。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int>ret;
if(root == nullptr)return ret;
stack<TreeNode*>st;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
st.pop();
ret.push_back(node->val);
if(node->left)st.push(node->left);
if(node->right)st.push(node->right);
}
reverse(ret.begin(),ret.end());
return ret;
}
};
94. 二叉树的中序遍历
- 不断遍历左结点直至为空,这期间不断push进栈,为空后开始往外吐,出栈,收集结果,然后转向当前结点右边,继续判断是否为空,决定是push left还是pop出来收集结果。
- 其实中间转向右边的过程,就是在收集中间结点的结果。只是在叶子结点体现为,right为空,然后接着pop出来,然后再取出top就是该叶子结点的父结点。然后cur=cur->right,转向右边,收集右孩子结果,同理。
- 如下图动画所示: 注意遍历的过程。

// 左中右
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int>ret;
if(root == nullptr)return ret;
stack<TreeNode*>st;
TreeNode* cur = root;
while(cur != nullptr || !st.empty()){
if(!cur){
// 收集
cur = st.top();
st.pop();
ret.push_back(cur->val);
cur = cur->right;
}else{
st.push(cur);
cur = cur->left;
}
}
return ret;
}
};
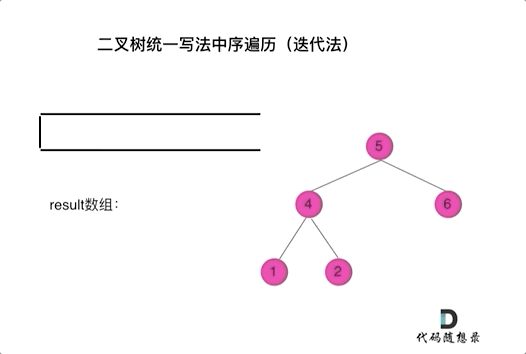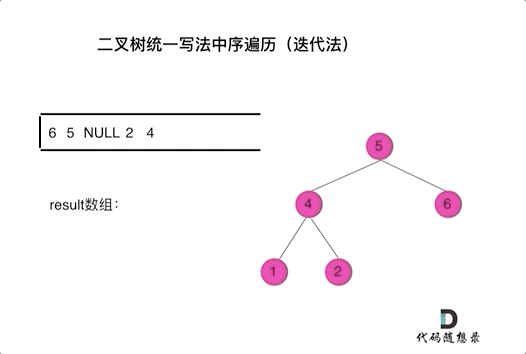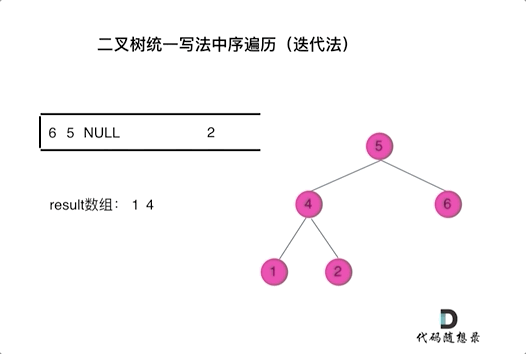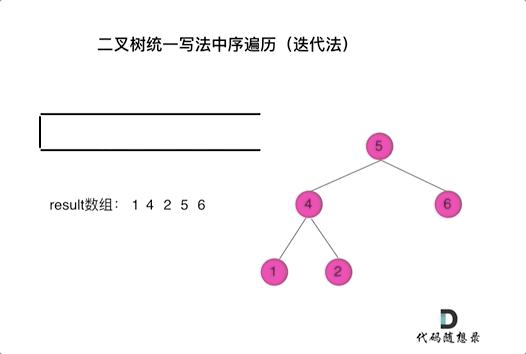
二叉树的统一迭代法遍历
94. 二叉树的中序遍历
- 从根结点开始遍历,while前先压入根结点,进入循环,开始判断,栈顶元素是否非空;
- 非空,先pop出来,然后先压入right(非空),压入当前结点,再压入一个null,之后压入left(非空)。
- 为空,先pop,然后取出top,再pop出来,收集结果。
- 如下图动画所示,没理解的话,自己画个数,然后跟着走一遍就懂啦。
- 如此写法, 二叉树的前/中/后序,只是两行代码的顺序不同。
- 可以统一理解为,
用null来标识收集结点,如果栈顶元素为null了,说明遍历到了叶子结点了(指的是第一次为null,回退过程中),开始回退收集结果。,说明要收集结果了,其实每个结点再被收集前,都会前pop出一个null(废话),不同的遍历顺序,改变黄当前结点压栈和压入null的时机不同,导致收集结果的顺序不同,从而完成不同的遍历顺序。
// 左中右
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int>ret;
stack<TreeNode*>st;
if(root != nullptr)st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
if(node != nullptr){
st.pop();
if(node->right)st.push(node->right);// 右
st.push(node);// 访问过中结点,但是还没处理,添加空结点作为标记。
st.push(nullptr);// 左
if(node->left)st.push(node->left);
}else{
st.pop();// 弹出空结点
node = st.top();
st.pop();
ret.push_back(node->val);
}
}
return ret;
}
};
144. 二叉树的前序遍历
// 中左右
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int>ret;
stack<TreeNode*>st;
if(root != nullptr)st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
if(node != nullptr){
st.pop();
if(node->right)st.push(node->right);// 右
if(node->left)st.push(node->left);
st.push(node);
st.push(nullptr);
}else{
st.pop();
node = st.top();
st.pop();
ret.push_back(node->val);
}
}
return ret;
}
};
145. 二叉树的后序遍历
// 左右中
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int>ret;
stack<TreeNode*>st;
if(root != nullptr)st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
if(node != nullptr){
st.pop();
st.push(node);// 中
st.push(nullptr);
if(node->right)st.push(node->right);// 右
if(node->left)st.push(node->left);// 左
}else{
st.pop();// 弹出空结点
node = st.top();
st.pop();
ret.push_back(node->val);
}
}
return ret;
}
};
二叉树的层序遍历
- 二叉树的层序遍历需要使用队列来实现,
队列先进先出,符合一层一层遍历的逻辑,同理,栈先进后出适合模拟先深度优先遍历,即递归的逻辑。
102. 二叉树的层序遍历
- 从根结点开始,将当前层的每一个结点的左右孩子push进队列。 下一层从头开始取,收集结果,接着push左右孩子。
- 使用队列
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*>que;
if(root != nullptr)que.push(root);
vector<vector<int>>ret;
while(!que.empty()){
int size = que.size();
vector<int>tmp;
for(int i =0; i < size;i++){
TreeNode* node = que.front();
que.pop();
tmp.push_back(node->val);
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
ret.push_back(tmp);
}
return ret;
}
};
- 递归
// - 没具体理解。
class Solution {
public:
void order(TreeNode* cur,vector<vector<int>>& ret,int depth){
if(cur == nullptr)return;// 终止条件
if(ret.size() == depth)ret.push_back(vector<int>());
ret[depth].push_back(cur->val);
order(cur->left,ret,depth+1);
order(cur->right,ret,depth+1);
}
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>>ret;
order(root,ret,0);
return ret;
}
};
107.二叉树的层次遍历 II
- 在上一题基础上反转即可
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*>que;
vector<vector<int>>ret;
if(root)que.push(root);
while(!que.empty()){
int size = que.size();
vector<int>tmp;
for(int i = 0; i < size;i++){
TreeNode* node = que.front();
que.pop();
tmp.push_back(node->val);
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
ret.push_back(tmp);
}
reverse(ret.begin(),ret.end());
return ret;
}
};
199. 二叉树的右视图
- 即收集每层的最右边结点值。
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*>que;
vector<int>ret;
if(root)que.push(root);
while(!que.empty()){
int size = que.size();
for(int i = 0; i < size ;i++){
TreeNode* node = que.front();
que.pop();
if(i == size-1)ret.push_back(node->val);
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
return ret;
}
};
637.二叉树的层平均值
- 计算每层和,求平均值。
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
queue<TreeNode*>que;
vector<double>ret;
if(root)que.push(root);
while(!que.empty()){
int size = que.size();
double sum = 0;
for(int i = 0; i < size ;i++){
TreeNode* node = que.front();
que.pop();
sum += node->val;
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
ret.push_back((double)sum/size);
}
return ret;
}
};
429.N叉树的层序遍历
- 没有区别,只是由左右孩子变成了孩子们。
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
queue<Node*>que;
if(root)que.push(root);
vector<vector<int>>ret;
while(!que.empty()){
int size = que.size();
vector<int>tmp;
for(int i = 0; i < size;i++){
Node* node = que.front();
que.pop();
tmp.push_back(node->val);//这里收集每层结果
for(int j = 0; j < node->children.size();j++){
if(node->children[j])que.push(node->children[j]);
}
}
ret.push_back(tmp);
}
return ret;
}
};
515.在每个树行中找最大值
- 收集每层的最大值。
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
queue<TreeNode*>que;
if(root)que.push(root);
vector<int>ret;
while(!que.empty()){
int size = que.size();
int tmpMax = INT_MIN;
for(int i = 0; i < size;i++){
TreeNode* node = que.front();
que.pop();
tmpMax = max(tmpMax,node->val);
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
ret.push_back(tmpMax);
}
return ret;
}
};
116.填充每个结点的下一个右侧结点指针
- 每层中,保存前一个结点,指向下一个。
class Solution {
public:
Node* connect(Node* root) {
queue<Node*>que;
if(root)que.push(root);
while(!que.empty()){
int size = que.size();
Node* prenode = NULL;
Node* node = NULL;
for(int i = 0; i < size;i++){
if(i == 0){
node= que.front();
que.pop();
prenode = node;// 注意这里-每层的第一个结点。
}else{
node = que.front();
que.pop();
prenode->next = node;// 上一个结点的next指向本结点
prenode = node;
}
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
prenode->next =NULL;// 最后一个结点的next指向null
}
return root;
}
};
117.填充每个结点的下一个右侧结点指针II
- 同上题,上道题指明是完全二叉树,本体只说明是二叉树,代码实现没区别。
class Solution {
public:
Node* connect(Node* root) {
queue<Node*>que;
if(root)que.push(root);
while(!que.empty()){
int size = que.size();
Node* node;
Node* prenode;
for(int i = 0; i < size;i++){
if(i == 0){
node = que.front();
que.pop();
prenode = node;
}else{
node = que.front();
que.pop();
prenode->next = node;
prenode = node;
}
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
return root;
}
};
104.二叉树的最大深度
- 模板题,增加一个变量记录层数即可。
class Solution {
public:
int maxDepth(TreeNode* root) {
queue<TreeNode*>que;
if(root)que.push(root);
int depth = 0;
while(!que.empty()){
int size = que.size();
depth++;
for(int i = 0;i < size; i++){
TreeNode* node = que.front();
que.pop();
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
return depth;
}
};
111.二叉树的最小深度
- 某一层的某个结点的左右孩子都为空,即出现了叶子结点,那么那层就是最小深度。
class Solution {
public:
int minDepth(TreeNode* root) {
queue<TreeNode*>que;
if(root)que.push(root);
int ret = 0;
int depth = 0;
while(!que.empty()){
int size= que.size();
depth++;
for(int i = 0; i < size ;i++){
TreeNode* node = que.front();
que.pop();
if(!node->left && !node->right)return depth;
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
return depth;
}
};
226. 翻转二叉树
- 递归法,使用前序法遍历
class Solution {
public:
// 参数&返回值
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr)return root;// 终止条件
// 单层递归逻辑
swap(root->left,root->right);// 中
invertTree(root->left);// 左
invertTree(root->right);// 右
return root;
}
};
- 迭代法
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*>st;
if(!root)return root;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();// 中
st.pop();
swap(node->left,node->right);
if(node->right)st.push(node->right);// 右
if(node->left)st.push(node->left);// 左
}
return root;
}
};
- 另一种迭代方法,二叉树的前/后/中序同一迭代方法。
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*>st;
if(!root)return root;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
if(node){
st.pop();
if(node->right)st.push(node->right);
if(node->left)st.push(node->left);
st.push(node);
st.push(nullptr);
}else{// 收集结果
st.pop();
node = st.top();
st.pop();
swap(node->left,node->right);
}
}
return root;
}
// 同一个迭代方式,收集了目标结点后(遍历顺序要求遍历的第一个结点),pop获取下一个结点,然后对该结点进行同样的操作,即。这种方式获取结点的值时,必然top为nullptr,然后再pop就是我们要的结点,获取结点的顺序由if(node)中控制,压栈,所以要与对应的遍历顺序反过来进栈。
};
- 同样,层序遍历也可以写这道题
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue<TreeNode*>que;
if(root)que.push(root);
while(!que.empty()){
int size = que.size();
for(int i = 0; i <size;i++){
TreeNode* node = que.front();
que.pop();
swap(node->left,node->right);
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
return root;
}
};
101. 对称二叉树
- 使用后序遍历,获取孩子的信息返回给根结点。
- 递归法
class Solution {
public:
bool compare(TreeNode* left,TreeNode* right){
// 也就是所,一切都相等的话,不会被下面这个几个调价卡住,会最终到达叶子结点的孩子,即nullptr,最后逐层返回true.
// 反之,中途被卡住,return false.
if(!left && !right)return true;// 最终从叶子结点返上来。为空,其实是叶子结点的孩子。
else if(!left && right)return false;
else if(left && !right)return false;
else if(left->val != right->val)return false;// 注意,这里的几个if判断顺序其实还是有点要求的,这个判断值是否相等的,要放到最后,因为只有经过上面几个的判断,我们才能保证,到达这里的不是空指针。
// 进行下一层的判断
bool outSide = compare(left->left,right->right);// 外侧
bool inSide = compare(left->right,right->left);// 内侧
return outSide && inSide;
}
bool isSymmetric(TreeNode* root) {
if(!root)return true;
return compare(root->left,root->right);
}
};
- 迭代法,层序遍历
class Solution {
public:
bool isSymmetric(TreeNode* root) {
queue<TreeNode*>que;
if(!root)return true;
que.push(root->left);
que.push(root->right);
while(!que.empty()){
TreeNode* leftNode = que.front();que.pop();
TreeNode* rightNode = que.front();que.pop();
if(!leftNode && !rightNode)continue;// 都为空,对称。必须要判断这步,同时也是说明到达叶子结点了(叶子结点的孩子)。
if(!leftNode || !rightNode || (leftNode->val != rightNode->val))return false;
que.push(leftNode->left);
que.push(rightNode->right);
que.push(leftNode->right);
que.push(rightNode->left);
}
return true;
}
};
100. 相同的树
- 与上题对称二叉树类似,只不过对比的是相同一边的结点是否相同。稍微修改即可AC。
class Solution {
public:
bool dfs(TreeNode* p,TreeNode* q){
if(!p && !q)return true;// 到底开始返回
else if(!p && q)return false;
else if(p && !q)return false;
else if(p->val != q->val)return false;
return dfs(p->left,q->left) && dfs(p->right,q->right);
}
bool isSameTree(TreeNode* p, TreeNode* q) {
return dfs(p,q);
}
};
572. 另一棵树的子树
- 相关参考-(补充)代码随想录中,57题题解,使用递归法
- 双层递归
class Solution {
public:
bool dfs(TreeNode* root,TreeNode* subRoot){// 递归,用于判断是否相等
if(!root && !subRoot) return true;
else if(!root && subRoot) return false;
else if(root && !subRoot)return false;
else if(root->val != subRoot->val)return false;// 学习到了,放到最后,保证不是空指针。
return dfs(root->left,subRoot->left) && dfs(root->right,subRoot->right);
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {// 递归,用于往下寻找子树。
if(!root)return false;// 为空判断,空结点没有left/right
return dfs(root,subRoot) || isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}
};
104.二叉树的最大深度
- 递归法
class Solution {
public:
int getDepth(TreeNode* node){
if(!node)return 0;// 从底部开始返回
// 单层递归逻辑,先求左子树深度,再求右字数深度,然后根据左右子树深度最大值+1求父结点深度。
int leftDep = getDepth(node->left);
int rightDep = getDepth(node->right);
return 1+max(leftDep,rightDep);
}
int maxDepth(TreeNode* root) {
return getDepth(root);
}
};
- 使用前序遍历的递归法
class Solution {
public:
int ret;
void getDepth(TreeNode* node,int depth){
ret = max(ret,depth);// 收集最大值结果
// 叶子结点返回
if(!node->left && !node->right)return ;
// 求左子树
if(node->left){
depth++;
getDepth(node->left,depth);
depth--;// 回溯
}
// 求右子树
if(node->right){
depth++;
getDepth(node->right,depth);
depth--;
}
// 简化一下,将以上两步写成这样,与上面等价。直接传depth+1相当于没改变本层递归中depth的值。
// 即,先++ 相当于传deoth+1,然后--,相当于没变。
//if(node->left)getDepth(node->left,depth+1);
//if(node->right)getDepth(node->right,depth+1);
}
int maxDepth(TreeNode* root) {
ret = 0;
if(!root)return 0;
getDepth(root,1);// 默认一层
return ret;
}
};
- 迭代法——使用层序遍历
class Solution {
public:
int maxDepth(TreeNode* root) {
queue<TreeNode*>que;
if(root)que.push(root);
int depth = 0;
while(!que.empty()){
int size = que.size();
depth++;
for(int i = 0 ; i < size;i++){
TreeNode* node = que.front();
que.pop();
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
return depth;
}
};
559. N 叉树的最大深度
class Solution {
public:
int maxDepth(Node* root) {
if(!root)return 0;// 终止条件
int depth = 0;
// 单层递归逻辑
for(int i = 0;i < root->children.size();i++){
depth = max(depth,maxDepth(root->children[i]));
}
return depth+1;// 层数++
}
};
111. 二叉树的最小深度
- 注意: 最小深度是从根结点到最近叶子结点的最短路径上的结点数量。
- 递归法
class Solution {
public:
int minDepth(TreeNode* root) {
if(!root) return 0;
int leftDep = minDepth(root->left);
int rightDep = minDepth(root->right);
// 注意最小高度是到叶子结点
if(root->left && !root->right)return leftDep+1;
if(!root->left && root->right)return rightDep+1;
return min(leftDep,rightDep)+1;
}
};
- 递归法-前序遍历,这个会更清晰些。
class Solution {
public:
int ret;
void getMinDepth(TreeNode* root,int depth){
if(!root->left && !root->right){// 感觉这里可以理解为中
ret = min(ret,depth);
return ;
}
// 左
if(root->left){
getMinDepth(root->left,depth+1);
}
// 右
if(root->right){
getMinDepth(root->right,depth+1);
}
}
int minDepth(TreeNode* root) {
ret = INT_MAX;
if(!root)return 0;
getMinDepth(root,1);
return ret;
}
};
- 迭代法-使用层序遍历
class Solution {
public:
int minDepth(TreeNode* root) {
queue<TreeNode*>que;
if(root)que.push(root);
int depth = 0;
while(!que.empty()){
int size = que.size();
depth++;
for(int i = 0;i < size;i++){
TreeNode*node = que.front();
que.pop();
if(!node->left && !node->right)return depth;
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
return depth;
}
};
222. 完全二叉树的结点个数
- 递归法
class Solution {
public:
int countNodes(TreeNode* root) {
if(!root)return 0;// 终止条件
// 单层递归逻辑
int lefts = countNodes(root->left);
int rights = countNodes(root->right);
return lefts+rights+1;
}
};
- 迭代法——层序遍历
class Solution {
public:
int countNodes(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
int result = 0;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
result++; // 记录结点数量
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};
110. 平衡二叉树
- 平衡二叉树,左右子树高度差不超过1
- 二叉树的
高度: 某结点距离叶子结点的距离。后序遍历,将左右孩子的情况返给父结点。- 二叉树的
深度: 某结点距离根结点的距离。前序遍历,向下遍历,直到根结点。- 补充
- 二叉树结点的深度:指从根结点到该结点的最长简单路径边的条数。
- 二叉树结点的高度:指从该结点到叶子结点的最长简单路径边的条数。
- 但leetcode中强调的深度和高度很明显是按照结点来计算的。
- 关于根结点的深度究竟是1 还是 0,不同的地方有不一样的标准,leetcode的题目中都是以结点为一度,即根结点深度是1。但维基百科上定义用边为一度,即根结点的深度是0,我们暂时以leetcode为准(毕竟要在这上面刷题)。
- 递归法
// 下面平衡了,上面也会平衡。反之,同理。
class Solution {
public:
int dfs(TreeNode* node){
if(!node)return 0;// 叶子结点高度为0
// 单层递归逻辑,判断左右子树是否平衡
int leftHeight = dfs(node->left);
if(leftHeight == -1)return -1;
int rightHeight = dfs(node->right);
if(rightHeight == -1)return -1;
// 求左右子树高度差
if(abs(rightHeight-leftHeight) > 1){// 不平衡啦
return -1;// 返回-1
}else{
return 1+max(leftHeight,rightHeight);
}
}
bool isBalanced(TreeNode* root) {
return dfs(root) == -1 ? false : true;
}
};
- 迭代法
- 使用栈模拟递归后序遍历,以每个结点为根结点,传递进去,
求该结点最大深度(叶子结点到根节点),即该结点的高度(距叶子结点的距离)。
- 即,以传递进来的这个结点为根结点的小树,求出来的最大深度,即根结点到叶子结点的距离,即为该结点在原树中的高度(距叶子结点的距离)。
- 然后层序遍历,看以每个结点为根结点的子树是否平衡。
- 或者使用后续遍历,感觉会有些浪费,于是我尝试直接传root->eft和root->right.但是仍有个别用例无法通过,不做追究了。
class Solution {
public:
int getHeight(TreeNode* node){
stack<TreeNode*>st;
if(node)st.push(node);
int depth = 0;
int ret = 0;// 收集最大结果即为最大深度,因为会回退。
while(!st.empty()){
TreeNode* node = st.top();
if(node){
st.pop();// 注意这里要先pop出来,再根据遍历顺序放入。
st.push(node);
st.push(nullptr);
if(node->right)st.push(node->right);
if(node->left)st.push(node->left);
depth++;
}else{
st.pop();
node = st.top();
st.pop();
depth--;// 回退
}
ret = max(ret,depth);// 收集
}
return ret;
}
bool isBalanced(TreeNode* root) {
queue<TreeNode*>que;
if(root)que.push(root);
while(!que.empty()){
int size = que.size();
for(int i = 0 ;i < size;i++){
TreeNode* node = que.front();
que.pop();
if(abs(getHeight(node->right)-getHeight(node->left))> 1){
return false;
}
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
return true;
}
};
- 上述跌打法中,使用stack后续遍历。
bool isBalanced(TreeNode* root) {
stack<TreeNode*>st;
if(!root)return true;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
st.pop();
if(abs(getHeight(node->left)-getHeight(node->right))> 1){
return false;
}
if(node->right)st.push(node->right);
if(node->left)st.push(node->left);
}
return true;
}
257. 二叉树的所有路径
- 递归
class Solution {
public:
void dfs(TreeNode* node,string &path,vector<string>&ret){
// 中,放到这里是因为要收集最后一个结点
path.push_back(node->val);
// 收集结果
if(!node->left && !node->right){
string tmp;
for(int i =0; i < path.size()-1;i++){// 收集前path.size()-1个
tmp += to_string(path[i]);
tmp += "->";
}
tmp += to_string(path[path.size()-1]);
ret.push_back(tmp);// 结果
return ;
}
// 左
if(node->left){
dfs(node->left,path,ret);
path.pop_back();
}
// 右
if(node->right){
dfs(node->right,path,ret);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string>ret;
if(!root)return ret;
string path;
dfs(root,path,ret);
return ret;
}
};
- 精简版
- 这时候,参数path不传递引用,否则无法达到回溯效果。
class Solution {
public:
// 非引用传递,传递path后return回来,并不会修改,即实际上回退回来,就相当于pop_back了(回退)。
void dfs(TreeNode* node,string path,vector<string>& ret){
path += to_string(node->val);// 中,收集
if(!node->left && !node->right){
ret.push_back(path);
return ;
}
if(node->left)dfs(node->left,path+"->",ret);
if(node->right)dfs(node->right,path+"->",ret);
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string>ret;
if(!root)return ret;
string path;
dfs(root,path,ret);
return ret;
}
};
- 或者修改为,注意体现回溯的地方。
class Solution {
public:
void dfs(TreeNode* node,string path,vector<string>& ret){
path += to_string(node->val);
if(!node->left && !node->right){
ret.push_back(path);
return ;
}
if(node->left){
path += "->";
dfs(node->left,path,ret);
path.pop_back();
path.pop_back();
}
if(node->right){
path += "->";
dfs(node->right,path,ret);
path.pop_back();
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string>ret;
if(!root)return ret;
string path;
dfs(root,path,ret);
return ret;
}
};
404. 左叶子之和
- 注意是叶子结点。
- 后序遍历,因为要根据孩子的值,返回给上面父结点。
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if(!root)return 0;
int leftV = sumOfLeftLeaves(root->left);// 左
int rightV = sumOfLeftLeaves(root->right);// 右
if(root->left && !root->left->left && !root->left->right){// 收集-中
leftV = root->left->val;
}
return leftV+rightV;
}
};
- 迭代法,无所谓遍历顺序,只需找到左叶子即可。
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
stack<TreeNode*>st;
if(!root)return 0;
st.push(root);
int ret = 0;
while(!st.empty()){
TreeNode* node = st.top();
st.pop();
if(node->left && !node->left->left && !node->left->right){
ret+=node->left->val;
}
if(node->right)st.push(node->right);
if(node->left)st.push(node->left);
}
return ret;
}
};
513. 找树左下角的值
- 就是最后一行第一个元素。
- 递归法,对遍历顺序没有要求,只要
左边优先即可。- 通过深度来判断是否为最后一行的第一个元素。深度最大的叶子结点肯定在最后一行。
class Solution {
public:
int ret;
int max_depth;
void dfs(TreeNode* node,int depth){
if(!node->left && !node->right){
if(depth > max_depth){
max_depth = depth;
ret = node->val;
}
return ;// 注意这里回退
}
if(node->left)dfs(node->left,depth+1);
if(node->right)dfs(node->right,depth+1);
// 展开回溯细节,可以将depth以引用方式传递,也可以不用。
// if(node->left){
// depth++;
// dfs(node->left,depth);
// depth--;
// }
// if(node->right){
// depth++;
// dfs(node->right,depth);
// depth--;
// }
}
int findBottomLeftValue(TreeNode* root) {
ret = 0;
max_depth = INT_MIN;
dfs(root,0);
return ret;
}
};
- 迭代法
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*>que;
if(root)que.push(root);
int ret = 0;
while(!que.empty()){
int size = que.size();
for(int i = 0; i < size;i++){
TreeNode* node = que.front();
que.pop();
if(i == 0)ret = node->val;// 收集每行第一个
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
return ret;
}
};
112. 路径总和
- 递归法
- 前中后续遍历都可以,因为也不涉及到中结点的处理逻辑,也就是中结点放到哪儿都行。没有要处理中结点(父结点)的需要。
class Solution {
public:
bool dfs(TreeNode* node,int target){
if(!node->left && !node->right && target == 0) return true;
if(!node->left && !node->right && target != 0) return false;
if(node->left){// 左
target -= node->left->val;
if(dfs(node->left,target))return true;
target += node->left->val;
}
if(node->right){// 右
target -= node->right->val;
if(dfs(node->right,target))return true;
target += node->right->val;
}
// 精简版
// if(node->left){
// if(dfs(node->left,target-node->left->val))return true;
// }
// if(node->right){
// if(dfs(node->right,target-node->right->val))return true;
// }
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root)return false;
// 注意上面递归中,每次调用时减去下一个要遍历的结点的值。
return dfs(root,targetSum-root->val);// 减去root->val
}
};
- 迭代法,也无序考虑遍历顺序。我们只需要在路上把经过的结点的值累加上来即可。并不需要对中结点有什么特殊处理,将值加上去就行了。累加的这步整合在了往下遍历结点,即往栈中push的过程中。
- 在实际的代码实现中,就是将父结点的值与要遍历的结点的值相加。求出来得到达该结点的值。
- 随着pop出该结点,再取得上一个结点,其实就是回溯的回退过程。
- 栈中储存的是结点,与到达该结点的这一路径上的值总和。
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root)return false;
stack<pair<TreeNode*,int>>st;
st.push(pair<TreeNode*,int>(root,root->val));
while(!st.empty()){
pair<TreeNode*,int> node = st.top();
st.pop();
if(!node.first->left && !node.first->right && targetSum == node.second)return true;
//压进去的时候顺便把值也算进去
if(node.first->right){// 右
st.push(pair<TreeNode*,int>(node.first->right,node.first->right->val+node.second));
}
if(node.first->left){// 左
st.push(pair<TreeNode*,int>(node.first->left,node.first->left->val+node.second));
}
}
return false;
}
};
113. 路径总和 II
- 同上一题,只不过将判断是否存在这样的路径,改成了收集这样的所有路径。
- 递归法
class Solution {
public:
vector<vector<int>>ret;
vector<int>path;
void dfs(TreeNode* node,int target){
if(!node->left && !node->right && target == 0){
ret.push_back(path);
return ;
}
// 这步加不加都行,因为到了叶子结点,下面两个if也是无法通过的。
if(!node->left && !node->right && target != 0)return ;
if(node->left){
path.push_back(node->left->val);
target -= node->left->val;// 本来想隐藏一下这步回溯过程的,但是还是写出来好理解些,因为path也涉及到回退。
dfs(node->left,target);
path.pop_back();
target += node->left->val;
}
if(node->right){
path.push_back(node->right->val);
target -= node->right->val;// 本来想隐藏一下这步回溯过程的,但是还是写出来好理解些,因为path也涉及到回退。
dfs(node->right,target);
path.pop_back();
target += node->right->val;
}
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if(!root)return ret;
path.push_back(root->val);
dfs(root,targetSum-root->val);
return ret;
}
};
- 迭代法,没想出来,这里略。
106.从中序与后序遍历序列构造二叉树
- 步骤:
- 在后序数组中找到根结点,然后在中序数组中完成切割。划分左右区间。
- 接着用上面求出的左右区间,再去切割后序数组。
- 在上面切割后的数组中再寻找中间元素(父结点)。
- 详细步骤:
- 如果数组大小为0的话,说明是空结点了。
- 如果不为空,那么取后序数组最后一个元素作为父结点元素。
- 找到上面找到的父结点的值在中序数组中的位置,作为切割点。
- 根据上面找到的切割点,切割中序数组,切成中序左数组和中序右数组(注意顺序)。
- 切割后序数组,切成后序左数组和后序右数组。
- 递归处理左区间和右区间。
- 核心要点:
- 后序遍历(左右中),中序遍历(左中右)。
- 根据后序遍历找到父结点,然后根据中序遍历,找到以此结点为父结点的左右子树区间,然后再根据左右子树区间,在后序遍历中再去划分左右子树的区间,再次根据两个区间找到其对应的父结点,即为第一次找到的父结点的左右子树。......
注意边界控制。C++迭代器,注意begin()指向第一个元素,end()指向最后一个元素的后面。更高效的做法是使用下标控制元素数组访问,而不是每次都创建新的数组。- 详细过程详见如下动画所示。

class Solution {
public:
TreeNode* dfs(vector<int>& inorder,vector<int>& postorder){
if(postorder.size() == 0)return nullptr;
int rootVal = postorder[postorder.size()-1];
TreeNode* root = new TreeNode(rootVal);
// 后序数组中就一个结点,说明没有子结点,直接返回以该值,构造出的结点。
if(postorder.size() == 1)return root;
// 找到该父结点在中序数组中的位置,然后进行左右子树的划分。
int index = 0;
for(;index < inorder.size();index++){
if(inorder[index] == rootVal)break;
}
// 根据该父结点在中序数组中的位置进行左右子树的子数组分割
// 注意使用如下该构造方法是左闭右开
// 注意begin()指向第一个元素,end()指向最后一个元素的后面
// 左[inorder.begin(),inordered.begin()+index)
vector<int>leftInOrder(inorder.begin(),inorder.begin()+index);
// 右[inorder.begin()+index+1,inordered.end())
vector<int>rightInOrder(inorder.begin()+index+1,inorder.end());
// 划分后序数组
// 首先将之前使用的去掉
postorder.resize(postorder.size()-1);
// 开始划分后序
// 根据上面中序数组划分出的左右子数组的个数,在原来后序数组上进行划分。
// 左[postorder.bein(),postorder.begin()+leftInOrder.size())
vector<int>leftPostOrder(postorder.begin(),postorder.begin()+leftInOrder.size());
// 右[postorder.begin()+leftInOrder.size(),postorder.end())
vector<int>rightPostOrder(postorder.begin()+leftInOrder.size(),postorder.end());
// 递归
root->left = dfs(leftInOrder,leftPostOrder);
root->right = dfs(rightInOrder,rightPostOrder);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.size() == 0 || postorder.size() == 0)return nullptr;
return dfs(inorder,postorder);
}
};
105. 从前序与中序遍历序列构造二叉树
- 与上题相类似。
class Solution {
public:
// 同 106,只不过将从后序遍历数组去父结点,改为了从中序遍历数组中获取。
TreeNode* dfs(vector<int>& preorder,vector<int>& inorder){
if(preorder.size() == 0)return nullptr;
int rootVal = preorder[0];
TreeNode* root = new TreeNode(rootVal);
// 仅一个元素,说明为叶子结点。
if(preorder.size() == 1)return root;
// 在中序数组中寻找该父结点
int index = 0;
for(;index < inorder.size();index++){
if(inorder[index] == rootVal)break;
}
// 划分中序数组
// 注意跌大气begin()指向的是容器首元素,end()指向的是最后一个元素的后面。
// 左-[inorder.begin(),inorder.begin()+index)
vector<int>leftInorder(inorder.begin(),inorder.begin()+index);
// 右-[inorder.begin()+index+1,inorder.end())
// 注意这里的+1,跳过父结点。
vector<int>rightInorder(inorder.begin()+index+1,inorder.end());
// 更新前序遍历数组,删除刚才被选走的结点。
// (ps: 其实我感觉不删除也可以,用下标来控制,但是貌似有点麻烦。)同理也可以不构造数组,改用下标控制。
preorder.erase(preorder.begin());
// 划分前序遍历数组
// 左-[preorder.begin(),preorder.begin()+leftInorder.size())
vector<int>leftPreorder(preorder.begin(),preorder.begin()+leftInorder.size());
// 右-[preorder.begin()+leftInorder.size(),preorder.end())
// 与上面划分中序数组不同,这里没有+1,是因为不用跳过元素,而是接着划分。
vector<int>rightPreorder(preorder.begin()+leftInorder.size(),preorder.end());
root->left = dfs(leftPreorder,leftInorder);
root->right = dfs(rightPreorder,rightInorder);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.size() == 0 || inorder.size() == 0)return nullptr;
return dfs(preorder,inorder);
}
};
654.最大二叉树
- 与上面根据遍历顺序构造二叉树的那量道题很类似,也是找数,分割。
- 根据具体的情况判断,递归中的终止条件,即需不需要判断==0 ==1......
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
TreeNode* node = new TreeNode(0);
if(nums.size() == 1){// 叶子结点直接返回
node->val = nums[0];
return node;
}
int maxV = 0;
int index =0;
for(int i = 0; i < nums.size() ;i++){
if(nums[i] > maxV){
index = i;
maxV = nums[i];
}
}
node->val = maxV;
// 构造左子树,前提是存在对应的数,确保在该数组中,该最大值左右还有至少一个数。
if(index > 0){
vector<int>vecLeft(nums.begin(),nums.begin()+index);
node->left = constructMaximumBinaryTree(vecLeft);
}
if(index < nums.size()-1){
vector<int>vecRight(nums.begin()+index+1,nums.end());
node->right = constructMaximumBinaryTree(vecRight);
}
return node;
}
};
- 优化,使用数组下标来访问原数组,减少时间与空间的开销。
- 注意观察与上面方法中,不同的条件控制if语句。
class Solution {
public:
// 给一个左闭右开的区间[left,right),right为上一个最大值
TreeNode* dfs(vector<int>& nums,int left,int right){
if(left >= right)return nullptr;// 没有结点啦
int index = left;
for(int i = left;i < right;i++){
if(nums[i] > nums[index]){
index = i;
}
}
TreeNode* node = new TreeNode(nums[index]);
node->left = dfs(nums,left,index);
node->right = dfs(nums,index+1,right);
return node;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return dfs(nums,0,nums.size());
}
};
617. 合并二叉树
- 递归
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if(!t1)return t2;// 都为空的情况其实也包含在这里了,都为空,返回t2,t2也是空。
if(!t2)return t1;
t1->val += t2->val;// 都存在,合并到t1上
// 递归
t1->left = mergeTrees(t1->left,t2->left);
t1->right = mergeTrees(t1->right,t2->right);
return t1;
}
};
- 迭代法,层序遍历。
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if(!t1)return t2;
if(!t2)return t1;
queue<TreeNode*>que;
que.push(t1);
que.push(t2);
// 以t1树为基准
while(!que.empty()){
TreeNode* n1 = que.front();
que.pop();
TreeNode* n2 = que.front();
que.pop();
// 此时两个结点值一定不为空
n1->val += n2->val;
// t1 t2左子树都不为空
if(n1->left && n2->left){
que.push(n1->left);
que.push(n2->left);
}
if(n1->right && n2->right){
que.push(n1->right);
que.push(n2->right);
}
if(!n1->left && n2->left){
n1->left = n2->left;
}
if(!n1->right && n2->right){
n1->right = n2->right;
}
}
return t1;
}
};
700. 二叉搜索树中的搜索
- 二叉搜索树,左子树值大于根节点,右子树值小于根节点。
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if(!root)return nullptr;
//if(root->val == val)return root;
if(root->val < val)return searchBST(root->right,val);
if(root->val > val)return searchBST(root->left,val);
return root;// 相等
}
};
- 迭代法
- 由于二叉搜索树的特殊性,我们不需要使用栈进行深度优先遍历,或者使用队列进行广度优先遍历。
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
while(root){
if(root->val > val)root = root->left;
else if(root->val < val)root = root->right;
else return root;
}
return nullptr;
}
};
98. 验证二叉搜索树
- 递归法1:递归遍历所有结点,
- 由于二叉搜索树的性质,我们将其按照中序遍历将每个结点的值都保存下来,如果为升序数组,说明为二叉搜索树,反之则不是。
class Solution {
public:
vector<int>v;
void dfs(TreeNode* node){
if(!node)return ;
dfs(node->left);
v.push_back(node->val);
dfs(node->right);
}
bool isValidBST(TreeNode* root) {
dfs(root);
for(int i = 1; i < v.size();i++){
if(v[i] <= v[i-1])return false;
}
return true;
}
};
- 递归法: 递归中直接判断是否有序
- 写递归的时候要将眼光放长远,用全局的视角来看,不能单纯的只局限于一块。
- 例如,本体不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了。
- 本题中使用中序遍历的核心思想在于,由于二叉搜索树的特性: 左孩子<父结点<右孩子,所以使用中序遍历,左->中->右,依次遍历每个值,下面第二种方法使用pre来保存前一个结点会更加直观,按照中序遍历的顺序遍历,如果前一个结点值大于等于当前结点值,则不是二叉搜索树,return false。即左孩子大于父结点,或者父结点大于右孩子,皆为非二叉搜索树。
- 使用变量保存最大值同理。只不过没那么直观,而且比较局限,假如根结点值为LONG_MIN,我们还得设置一个比他还小的值。
class Solution {
public:
long long maxV = LONG_MIN;
bool isValidBST(TreeNode* root){
if(!root)return true;
bool leftV = isValidBST(root->left);
// 中序遍历,验证遍历的元素是不是从小到大的。
if(root->val > maxV){
maxV = root->val;
}else return false;
bool righV = isValidBST(root->right);
return leftV && righV;
}
};
- 优化
- 关键是用pre记录前一个结点。
class Solution {
public:
TreeNode* pre = nullptr;// 记录root的前一个结点,左/右
bool isValidBST(TreeNode* root){
if(!root)return true;
bool leftV = isValidBST(root->left);
if(pre != nullptr && pre->val >= root->val)return false;
pre = root;
bool righV = isValidBST(root->right);
return leftV && righV;
}
};
- 迭代-中序遍历。
class Solution {
public:
bool isValidBST(TreeNode* root) {
if(!root)return true;
stack<TreeNode*>st;
TreeNode* cur = root;
TreeNode* pre = nullptr;//记录前一个结点
while(!st.empty() || cur){
if(!cur){
cur = st.top();
st.pop();
if(pre && cur->val <= pre->val)return false;
pre = cur;
cur = cur->right;
}else{
st.push(cur);
cur = cur->left;
}
}
return true;
}
};
530.二叉搜索树的最小绝对差
- 递归: 中序遍历,转换为升序数组,遍历,即可求出。两两求差值即可。
class Solution {
public:
vector<int>nums;
void dfs(TreeNode* root){
if(!root)return ;
dfs(root->left);
nums.push_back(root->val);
dfs(root->right);
}
int getMinimumDifference(TreeNode* root) {
int ret = INT_MAX;
dfs(root);
for(int i = 1; i < nums.size();i++){
ret = min(ret,nums[i]-nums[i-1]);
}
return ret;
}
};
- 同上一题的其中一个做法,用一个指针来记录前一个结点。
class Solution {
public:
TreeNode* pre = nullptr;
int ret = INT_MAX;
void dfs(TreeNode* root){
if(!root)return ;
dfs(root->left);
if(pre)ret = min(ret,root->val-pre->val);
pre = root;
dfs(root->right);
}
int getMinimumDifference(TreeNode* root) {
dfs(root);
return ret;
}
};
- 迭代法-栈
class Solution {
public:
int getMinimumDifference(TreeNode* root) {
int ret = INT_MAX;
stack<TreeNode*>st;
TreeNode* pre = nullptr;
TreeNode* cur = root;
while(!st.empty() || cur){
if(cur){
st.push(cur);
cur = cur->left;
}else{// pop收集结果
cur = st.top();
st.pop();
if(pre)ret = min(ret,cur->val-pre->val);
pre = cur;
cur = cur->right;
}
}
return ret;
}
};
501.二叉搜索树中的众数
- 好好利用二叉搜索树的性质。
- 使用两个变量分别记录当前元素出现的次数,和当前出现过的最大元素次数。
- 如果等于之前最大出现的次数,结果集加入当前结点。
- 如果大于之前出现的最大次数,更新最大次数记录,清空结果集,之后结果集中加入当前结点。
- 递归: 注意其中很关键的一步,如果发现更大的出现次数,记得删除之前ret中保存的结点。
class Solution {
public:
vector<int>ret;
TreeNode* pre = nullptr;
int max_count = 0;
int count = 0;
void dfs(TreeNode* root){
if(!root)return ;
dfs(root->left);
if(!pre)count = 1;
else if(pre->val == root->val)count++;
else count = 1;
if(count == max_count){
ret.push_back(root->val);
}
if(count > max_count){
max_count = count;
ret.clear();
ret.push_back(root->val);
}
pre = root;
dfs(root->right);
}
vector<int> findMode(TreeNode* root) {
if(!root)return ret;
dfs(root);
return ret;
}
};
- 迭代
- 此方法使得我们无需遍历两次,遍历两次是因为,众数可能会有多个。
class Solution {
public:
vector<int> findMode(TreeNode* root) {
TreeNode* pre = nullptr;
TreeNode* cur = root;
vector<int>ret;
stack<TreeNode*>st;
int count = 0;
int max_count = 0;
while(!st.empty() || cur){
if(cur){
st.push(cur);
cur = cur->left;
}else{
cur = st.top();
st.pop();
if(!pre)count = 1;
else if(pre->val == cur->val)count++;
else count = 1;
if(count == max_count){
ret.push_back(cur->val);
}
if(count > max_count){
max_count = count;
ret.clear();
ret.push_back(cur->val);
}
pre = cur;
cur = cur->right;
}
}
return ret;
}
};
236. 二叉树的最近公共祖先
- 注意理解,我们不是说要从下网上遍历,而是利用递归,一层一层往上返回,来解决此问题。
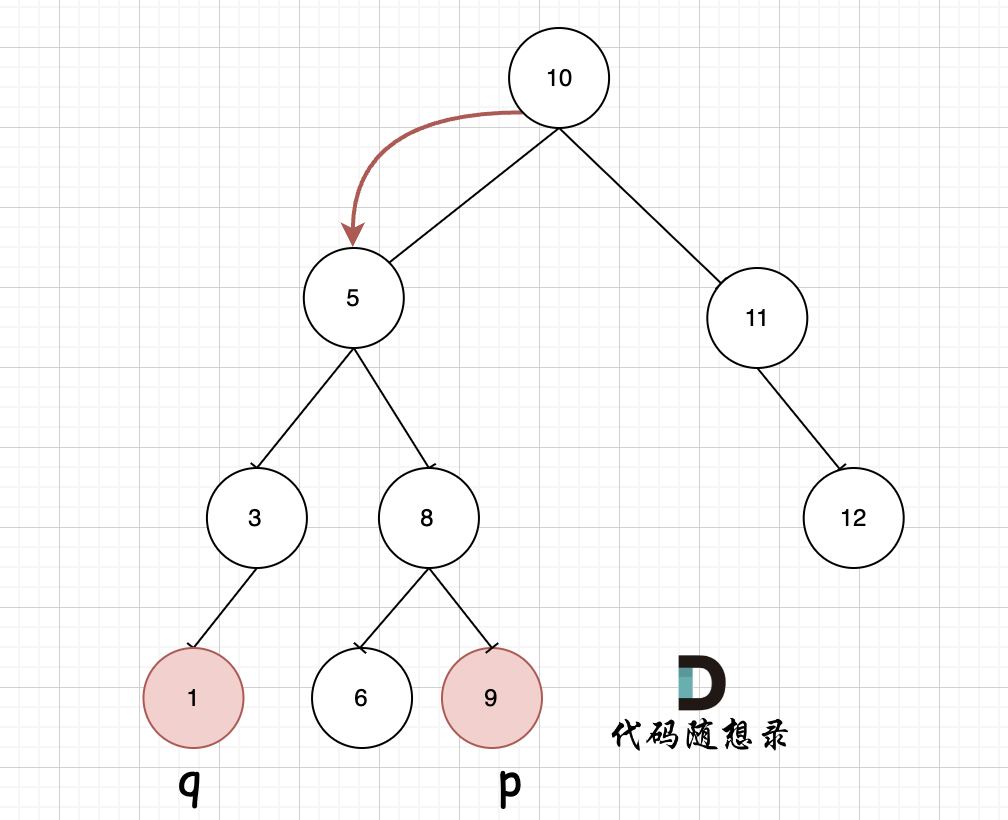
- 找到p or q,就向上返回,如果左右子树都不为空说明两个都找到了,接着返回,反之,只找到了一个即有一个不为空,说明目标结点由该结点返回。如下图所示:

- 图中结点10的左子树返回null,右子树返回7结点,那么此时结点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
- 如果找到一个结点,发现左子树出现结点p,右子树出现结点q,或者 左子树出现结点q,右子树出现结点p,那么该结点就是结点p和q的最近公共祖先。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root || root == p || root == q)return root;
// 这里补充一点,加入我们在左子树中找到目标结点了,仍然会继续遍历右子树。
TreeNode* left_t = lowestCommonAncestor(root->left,p,q);
TreeNode* right_t = lowestCommonAncestor(root->right,p,q);
if(left_t && right_t)return root;
else if(left_t && !right_t)return left_t;
else if(!left_t && right_t)return right_t;
else return NULL;
}
};
235. 二叉搜索树的最近公共祖先
- 递归法
- 利用二叉搜搜数的性质,我们得到解题关键: 从上往下遍历,当第一次遇到结点的值是在[p,q]区间的,说明该结点就是p和q的最近公共祖先。
- 不需要遍历整棵树,找到结果直接返回。
- 判断条件调整往左右子树遍历如下图所示:
- 不知道p q 谁大,所以都要判断。
- if(cur->val > p->val && cur->val > q->val)// 目标区间在左子树上
- if(cur->val < p->val && cur->val < q->val)// 目标区间在右子树上
- cur->val <= p->val && cur->val >= q->val 或 cur->val >= p->val && cur->val <= q->val // cur是公共祖先
class Solution {
public:
TreeNode* dfs(TreeNode* cur,TreeNode* p,TreeNode* q){
if(cur == NULL)return cur;
if(cur->val > p->val && cur->val > q->val){// 目标区间在左子树上,大于两个结点,往左遍历,相当于找一个更小的结点。往右相当于找一个更大的结点,使cur指向的结点的值能在p,q所构建的区间里。
TreeNode* left = dfs(cur->left,p,q);
if(left)return left;
}
if(cur->val < p->val && cur->val < q->val){// 目标区间在右子树上
TreeNode* right = dfs(cur->right,p,q);
if(right)return right;
}
// cur就是公共祖先
// cur->val <= p->val && cur->val >= q->val 或
// cur->val >= p->val && cur->val <= q->val
return cur;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
return dfs(root,p,q);
}
};
- 精简一些的版本:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// 因为题目说肯定可以找到,所以不用判断为空条件
if(root->val > p->val && root->val > q->val){
return lowestCommonAncestor(root->left,p,q);
}
if(root->val < p->val && root->val < q->val){
return lowestCommonAncestor(root->right,p,q);
}
return root;
}
};
- 补充: 如果递归函数有返回值,如何区分要搜索一条边,还是搜索整个树。
- 搜索一条边的写法:
if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;
- 搜索整棵树的写法
left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;
- 迭代法
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
while(root){
if(root->val > p->val && root->val > q->val)root = root->left;
else if(root->val < p->val && root->val < q->val)root = root->right;
else return root;
}
return root;
}
};
701.二叉搜索树中的插入操作
- 递归法1: 递归函数有返回值,遇到空结点,插入。
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root){// 到空节点了,说明该插入了
TreeNode* node = new TreeNode(val);
return node;
}
if(root->val > val)root->left= insertIntoBST(root->left,val);
if(root->val < val)root->right = insertIntoBST(root->right,val);
return root;
}
};
- 递归法2:递归函数无返回值,使用一个结点来保存上一个结点
class Solution {
public:
TreeNode* pre = nullptr;
void dfs(TreeNode* cur,int val){
if(!cur){
TreeNode* node = new TreeNode(val);
if(pre->val > val)pre->left = node;
else pre->right = node;
return ;
}
// 记录前一个结点
pre = cur;
// 其实在下面两个if语句中,调用完递归函数后,可以直接return
// 因为cur->val只能满足一下两个情况的一种。
if(cur->val > val)dfs(cur->left,val);
if(cur->val < val)dfs(cur->right,val);
}
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root){
TreeNode* node = new TreeNode(val);
return node;
}
dfs(root,val);
return root;
}
};
- 迭代
- 使用两个指针,一个负责遍历,一个记录父结点。注意这两个指针的使用技巧。
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
TreeNode* node = new TreeNode(val);
if(!root){
return node;
}
TreeNode* cur = root;
TreeNode* pre = nullptr;
while(cur){
pre = cur;
if(cur->val > val)cur = cur->left;
else cur = cur->right;
}// cur遍历到叶子结点
// 插入
if(pre->val > val)pre->left = node;
else pre->right = node;
return root;
}
};
450.删除二叉搜索树中的节点
- 不同于上一题的插入操作,本体涉及到要结构调整了。
- 分情况进行讨论:
- 没找到删除的结点:
- 情况1: 没找到要删除的结点,遍历到空节点返回。
- 找到了要删除的结点
- 情况2: 左右孩子都为空(叶子结点),直接删除该结点,返回NULL。
- 情况3: 删除结点的左孩子为空,右孩子不为空,删除该结点,右孩子补位,返回右孩子为根结点。
- 情况4: 删除结点的右孩子为空,左孩子不为空,删除该结点,左孩子补位,返回做孩子为根节点。
- 情况5:
删除结点的左右孩子都不为空,则将删除结点的左子树,放到删除结点的右子树的最左面结点的左孩子上,返回删除结点右孩子为新的根结点。如下图动画所示:
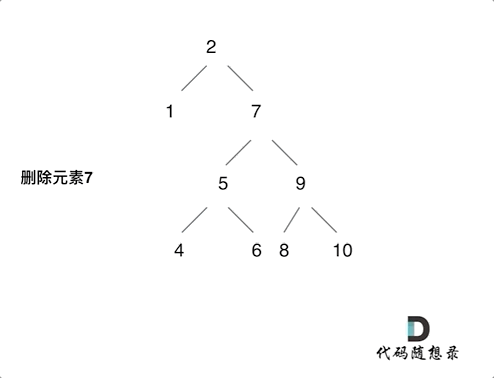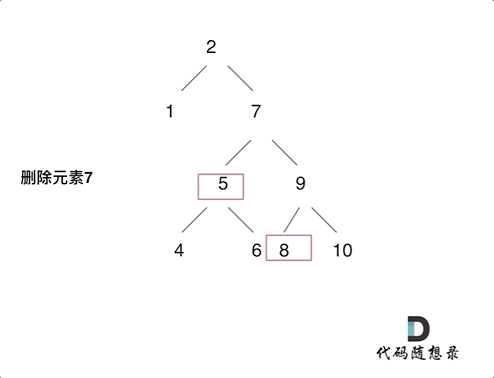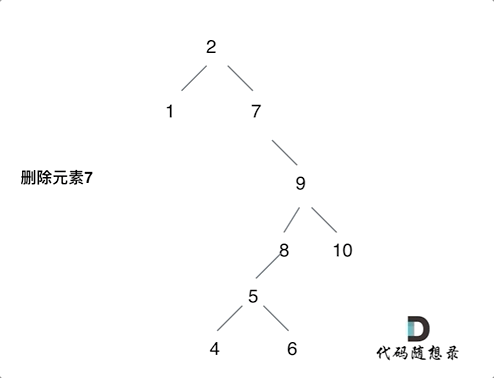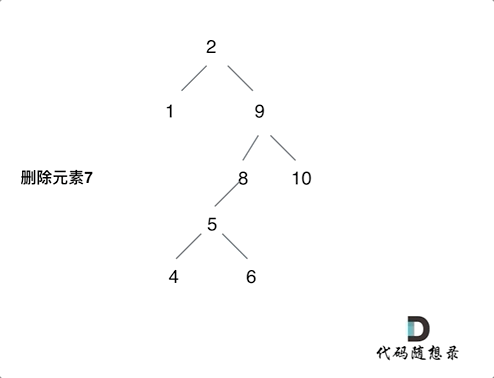
- 注意,本题删除结点,对遍历顺序没要求。
- 迭代法
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root) return root;// 没找到要删除的结点
// 找到要删除的结点
if(root->val == key){
if(!root->left && !root->right){// 左右孩子都为空
delete root;
return nullptr;
}else if(!root->left){// 左孩子为空
TreeNode* right_node = root->right;
delete root;
return right_node;
}else if(!root->right){// 右孩子为空
TreeNode* left_node = root->left;
delete root;
return left_node;
}else{// 左右孩子都不为空
// 把左子树,放到右孩子最左边结点的左孩子处。
TreeNode* cur = root->right;
while(cur->left){
cur = cur->left;
}
cur->left = root->left;
TreeNode* tmp = root;
root = root->right;// 注意更新该结点
delete tmp;
return root;
}
}
// 递归
if(root->val > key)root->left = deleteNode(root->left,key);// 要删除的结点在左子树
if(root->val < key)root->right = deleteNode(root->right,key);// 要删除的结点在右子树
return root;
}
};
- 通用的删除方式
- 不使用搜索树的性质,遍历整棵树,用交换值的操作来删除目标结点。
- 代码中,对要删除的结点进行了两步操作:
- 第一次和目标结点的右子树最左面结点进行交换,。
- 第二次直接被nullptr覆盖。
- 这种方法不好理解,可以结合下图思考一下。
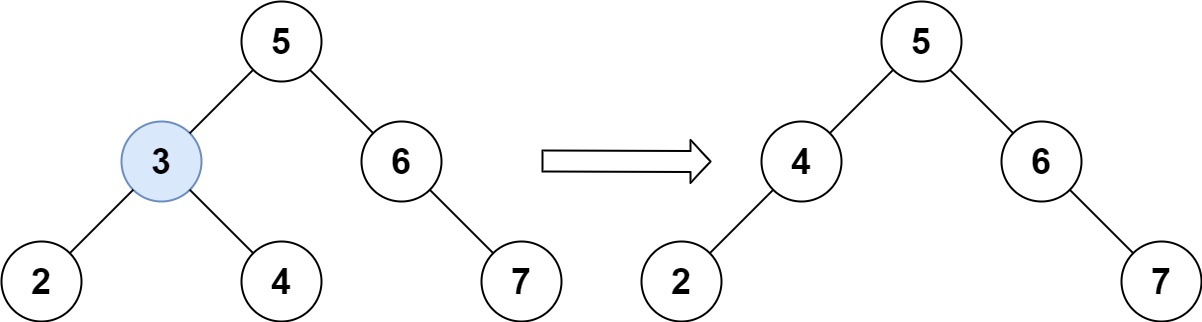
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root)return nullptr;
if(root->val == key){
if(!root->right) {// 第二次操作,起到最终删除的作用。
return root->left;
}
TreeNode* cur = root->right;
while(cur->left){
cur = cur->left;
}
swap(root->val ,cur->val);// 第一次操作,交换目标值交换到的右子树最左面的结点上。
}
root->left = deleteNode(root->left,key);
root->right = deleteNode(root->right,key);
return root;
}
};
- 迭代法
class Solution {
public:
// 对要删除的结点进行处理,返回以此结点父结点,处理完之后的结点结果。
TreeNode* deleteOneNode(TreeNode* target){// 删除target结点
if(!target){// 只有一个根结点,返回nullptr
delete target;
return nullptr;
}
if(!target->right)return target->left;// 右孩子空
if(!target->left)return target->right;// 左孩子空
// 左右孩子都不为空
TreeNode* cur = target->right;
// 将左子树放到右子树的最左面的结点的左孩子
while(cur->left){
cur = cur->left;
}
cur->left = target->left;
return target->right;
}
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root)return nullptr;
TreeNode* cur = root;
TreeNode* pre = nullptr;// 保存目前结点的父结点
while(cur){
if(cur->val == key)break;// 找到要删除的结点了
pre = cur;
if(cur->val > key)cur = cur->left;
else cur = cur->right;
}
if(!pre)return deleteOneNode(cur);
// 判断要删除的cur是左孩子还是右孩子
if(pre->left && pre->left->val == key){// 左
pre->left = deleteOneNode(cur);
delete cur;
}
if(pre->right && pre->right->val == key){
pre->right = deleteOneNode(cur);
delete cur;
}
return root;
}
};
669. 修剪二叉搜索树
- 注意二叉搜索树的性质,如果根结点小于low,说明左子树都小于low,同理,如果根节点大于high,说明右子树都大于high。
- 递归法
- 注意理解其中递归步骤的作用。
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(!root)return nullptr;
if(root->val < low){// 根结点的的值小于low
// 直接舍弃左子树,向上层返回右子树
return trimBST(root->right,low,high);
}
if(root->val > high){// 根结点的值大于high
// 直接舍弃右子树,返回左子树
return trimBST(root->left,low,high);
}
// 下面两行代码,用于接住下面层,返回满足条件的结点
root->left = trimBST(root->left,low,high);
root->right = trimBST(root->right,low,high);
return root;
}
};
- 迭代法
- 核心思想: 从下面拿到符合这个范围的结点。
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(!root)return nullptr;
// 处理头结点
while(root && (root->val < low || root->val > high)){
if(root->val < low)root = root->right;
else root = root->left;
}
TreeNode* cur = root;// 此时root->val已在[low,high]范围内
// 处理左子树,小于low的情况,左子树中的结点不可能大于high
while(cur){
while(cur->left && cur->left->val < low){
cur->left = cur->left->right;// 拿个大的上来
}
cur = cur->left;
}
cur = root;
// 处理右子树,大于high的情况,右子树中的结点不可能小于low
while(cur){
while(cur->right && cur->right->val > high){
cur->right = cur->right->left;
}
cur = cur->right;
}
return root;
}
};
108.将有序数组转换为二叉搜索树
- 递归法
- 核心思想不断分割数组,进行构造。类似上面的用xx序遍历中构造二叉树。
class Solution {
public:
// 左闭右闭区间
TreeNode* dfs(vector<int>&nums,int left,int right){
if(left > right)return nullptr;
int mid = left + (right-left)/2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = dfs(nums,left,mid-1);
root->right= dfs(nums,mid+1,right);
return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
return dfs(nums,0,nums.size()-1);
}
};
- 迭代法
- 使用三个队列来模拟,一个队列放遍历的节点,一个队列放左区间下标,一个队列放右区间下标。
- 层序遍历的思想,遍历每个结点的时候,将下层要用的结点放入(即孩子),然后依次取出,赋值。
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
if(nums.size() == 0)return nullptr;
TreeNode* root = new TreeNode(0);
queue<TreeNode*>nodeQue;
queue<int>leftQue;
queue<int>rightQue;
nodeQue.push(root);
leftQue.push(0);
rightQue.push(nums.size()-1);
while(!nodeQue.empty()){
TreeNode* cur = nodeQue.front();
nodeQue.pop();
int left = leftQue.front();
leftQue.pop();
int right = rightQue.front();
rightQue.pop();
int mid = left+(right-left)/2;
cur->val = nums[mid];
if(left <= mid-1){
cur->left = new TreeNode(0);
nodeQue.push(cur->left);
leftQue.push(left);
rightQue.push(mid-1);
}
if(right >= mid+1){
cur->right = new TreeNode(0);
nodeQue.push(cur->right);
leftQue.push(mid+1);
rightQue.push(right);
}
}
return root;
}
};
538.把二叉搜索树转换为累加树
- 递归法
- 从示例图中我们可以看出,结点的值的累加是按照“右中左”这个顺序的。
- 本题我们依然只用一个指向前一个结点的指针来辅助累加。我们没必要保存结点,保存一个值即可。
class Solution {
public:
int pre = 0;// 保存前一个结点的值
void dfs(TreeNode* root){
if(!root)return ;
dfs(root->right);
root->val += pre;
pre = root->val;// 更新前一个结点的值。
dfs(root->left);
}
TreeNode* convertBST(TreeNode* root) {
dfs(root);
return root;
}
};
- 迭代法
- 中序遍历模板题,不过要从左中右变成右中左。
class Solution {
public:
TreeNode* convertBST(TreeNode* root) {
stack<TreeNode*>st;
TreeNode* cur = root;
int pre = 0;
while(!st.empty() || cur){
if(cur){// 不为空
st.push(cur);
cur = cur->right;
}else{
cur = st.top();
st.pop();
cur->val += pre;
pre = cur->val;
cur = cur->left;
}
}
return root;
}
};
- 总结:
- 涉及到二叉树的构造,无论普通二叉树还是二叉搜索树,都是前序,先构造中结点。
- 求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
- 求二叉搜索树的属性,一定是中序,要不白瞎了有序性了。
感悟
- 不光是对二叉树的二刷感觉,也包括前面几张吧,刚才写到最后一道题突然有的这个想法,以后刷完一张进行一些小的感悟总结。
二叉树中章节中,相对于迭代,递归有时候会更好理解,部分题用到了马上要刷的回溯算法。
几乎每个题都用了迭代和递归两种方法,加上最近事情有些多,耗费的时间还是挺多的,接下来要注意看每章中的每周总结,感觉前面看的不是认真,还有就是注意每天的刷题时间,合理规划下。


评论区