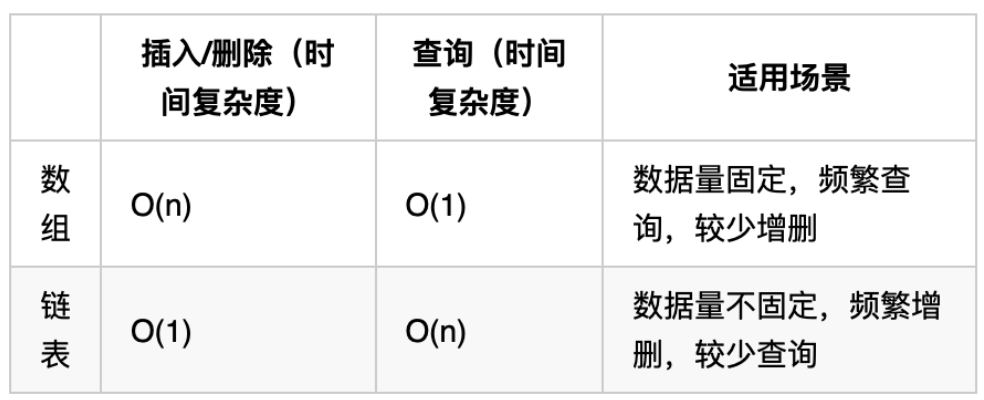
链表

《代码随想录》
前言

C++定义链表结点方式

struct node{
    int val;
    struct node* next;
    node(int v):val,next(nullptr){}
};

与数组对比

下面题目大部分时间复杂度如上图为O(n)
203. 移除链表元素

头结点和非头结点分开判断删除

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        // 删除头结点
        while(head && head->val == val){
            ListNode* tmp = head;
            head = head->next;
            delete tmp;
        }

        // 删除非头结点
        ListNode* cur = head;
        while(cur && cur->next){
            if(cur->next->val == val){
                ListNode* tmp = cur->next;
                cur->next = tmp->next;
                delete tmp;
            }else{
                cur = cur->next;
            }
        }
        return head;
    }
};

创建一个临时头结点,所有元素以统一方式删除。

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* tmpHead = new ListNode();// 创建一个临时头结点
        tmpHead->next = head;
        ListNode* cur = tmpHead;
        while(cur->next){
            if(cur->next->val == val){
                ListNode* tmp = cur->next;
                cur->next = tmp->next;
                delete tmp;
            }else{
                cur = cur->next;
            }
        }
        return tmpHead->next;
    }
};

707.设计链表

重点是index从0开始，可以想象成数组，索引从0开始。

如果还是没明白index，就去看示例。

class MyLinkedList {
public:
    struct node{
        int val;
        struct node* next;
        node(int v):val(v),next(nullptr){}
    };
    MyLinkedList() {
        m_size = 0;
        m_head = new node(0);
    }

    int get(int index) {
        if(index < 0 || index > m_size-1){
            return -1;
        }
        node* cur = m_head->next;
        while(index--){
            cur = cur->next;
        }// 循环结束，落到目标结点
        return cur->val;
    }

    void addAtHead(int val) {
        node* newNode = new node(val);
        node* tmp = m_head->next;
        m_head->next = newNode;
        newNode->next = tmp;
        m_size++;
    }

    void addAtTail(int val) {
        node* newNode = new node(val);
        node* cur = m_head;
        while(cur->next){
            cur = cur->next;
        }// 循环结束落到目标的前一个结点
        cur->next = newNode;
        newNode->next = nullptr;
        m_size++;
    }

    // 在索引为index的结点前添加值为val的结点
    // 本链表相当于数组，索引从0开始。
    // 示例: addAtIndex(1,1),即在索引为1的结点前插入值为1的结点。
    // m_size为当前实际有的元素数量，比最大索引小1

    // 以下情况:
    // index == m_size;尾插
    //  0 <= index <m_size 插入到index前
    // index > m_size不进行插入
    // index < 0 头插
    void addAtIndex(int index, int val) {
         if(index < 0){
            addAtHead(val);
            return ;
        }
        if(index > m_size){
            return;
        }
        if(index == m_size){
            addAtTail(val);
            return ;
        }
        node* newnode = new node(val);
        node* cur = m_head;
        while(index--){
            cur = cur->next;
        }// 循环结束，落到目标的前一个结点。
        node* tmpNext = cur->next;
        cur->next = newnode;
        newnode->next = tmpNext;
        m_size++;   
    }

    void deleteAtIndex(int index) {
        if(index < 0 || index > m_size-1){
            return ;
        } 
        node* cur = m_head;
        while(index--){
            cur = cur->next;
        }// 落到目标前一个结点
        node* tmp = cur->next;
        cur->next =  tmp->next;
        delete tmp;
        m_size--;
    }
private:
    int m_size;
    struct node* m_head;
};
// 原来他妈的题目说的第几个节点是指第几个索引！！！！——来自评论区

206.反转链表

双指针法

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* tmp = nullptr;// 保存下一个结点
        ListNode* cur = head;// 快指针
        ListNode* pre = nullptr;// 慢指针
        while(cur){
            tmp = cur->next;// 保存下一个结点
            cur->next = pre;// 调转方向
            pre = cur;// 更新慢指针-cur==nullptr就进不来循环了，所以最后一次pre肯定被置为原来的最后一个结点。
            cur = tmp;// 更新快指针
        }
        return pre;
    }
};

递归: 递归的过程即双指针中for循环内容。

class Solution {
public:
    ListNode* reverse(ListNode* cur,ListNode* pre){
        if(cur == nullptr)return pre;
        ListNode* temp = cur->next;
        cur->next = pre;
        // 递归就是做了这两个工作
        // pre = cur;
        // cur = temp;
        return reverse(temp,cur);
    }
    ListNode* reverseList(ListNode* head) {
        ***
        ## [24. 两两交换链表中的节点](https://leetcode.cn/problems/swap-nodes-in-pairs/)
        return reverse(head,nullptr);
    }
};

24. 两两交换链表中的节点

详情见注释

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* tmpHead = new ListNode(0);
        tmpHead->next = head;
        ListNode* cur = tmpHead;
        while(cur->next && cur->next->next){
            ListNode* tmp = cur->next;// 保存第一个结点
            ListNode* tmp1 = cur->next->next->next;// 保存第二个结点的后面一个

            cur->next = tmp->next;// 第二个变第一个
            cur->next->next = tmp;// 第一个变第二个
            tmp->next = tmp1;// 第二个链上之前第二个的后面一个        
            cur = cur->next->next;// 移动两下
            // 即每次都有“哨兵”结点，第一次为人为构造的，之后为上一次遍历的第二个结点。
        }
        return tmpHead->next;
    }
};

19. 删除链表的倒数第 N 个结点

快慢指针

创建虚拟头结点，这样可以使链表中的所有元素可以统一进行管理。

如果先让快指针走n步，然后快慢指针同时走，直到fast == nullptr,此时，slow所指向的正是要删除的导数第n个结点。

要删除，所以我们需要让fast再多走一步，即走n+1步，再让他们同时移动，直到fast == nullptr,此时slow正指向是要删除结点的前一个结点。

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* tmpHead = new ListNode(0);
        tmpHead->next = head;
        ListNode* fast = tmpHead;
        ListNode* slow = tmpHead;
        n++;// 安全起见，先加加，防止  之后再多移动一步移动空指针。
        // 但实际上因为题目中给了1<=n<=sz,所以那样写也不影响。
        while(n-- && fast)fast = fast->next;
        while(fast){
            slow = slow->next;
            fast = fast->next;
        }  
        ListNode* delNode = slow->next;
        slow->next = delNode->next; 
        delete delNode;
        return tmpHead->next;// 注意返回的是虚拟头结点的next,因为使用了虚拟头结点来统一管理所有结点。 
        // 刚才想了一下为什么不能返回head,因为有可能head被删掉啦。
    }
};

面试题 02.07. 链表相交

相同题目-160. 相交链表

解题步骤:

分别求出两个链表的长度

求出长度的差值，将两个链表按结尾对齐

同时遍历两个链表，指针相同则返回，反之一直没找到，返回NULL。

开始没想懂为什么要尾部对齐，看不懂就看题目给的示例图。

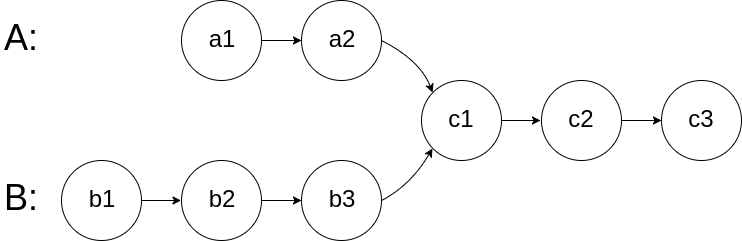
可以看出，在某一个相同的节点之后，两个链表的剩余结点都是相等的。所以要尾对齐。即公共尾部。

// 时间复杂度: O(n+m)
// 空间复杂度: O(1)
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        int lenA = 0;
        int lenB = 0;
        while(curA){
            curA = curA->next;
            lenA++;
        }
        while(curB){
            curB = curB->next;
            lenB++;
        }
        curA = headA;
        curB = headB;
        if(lenB > lenA ){// 使得A为长的字符串
            swap(lenA,lenB);
            swap(curA,curB);
        }
        int gep = lenA - lenB;
        while(gep--){
            curA = curA->next;
        }// 末尾对齐
        while(curA){
            if(curA == curB)return curA;
            curA = curA->next;
            curB = curB->next;
        }
        return NULL;
    }
};

双指针

都走一遍A+B

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(headA ==NULL || headB == NULL)return NULL;
        ListNode* curA = headA;
        ListNode* curB = headB;
        while(curA != curB){
            curA = curA == NULL ?headB:curA->next;
            curB = curB == NULL ?headA:curB->next;
        }
        return curA;
    }
};

142. 环形链表 II

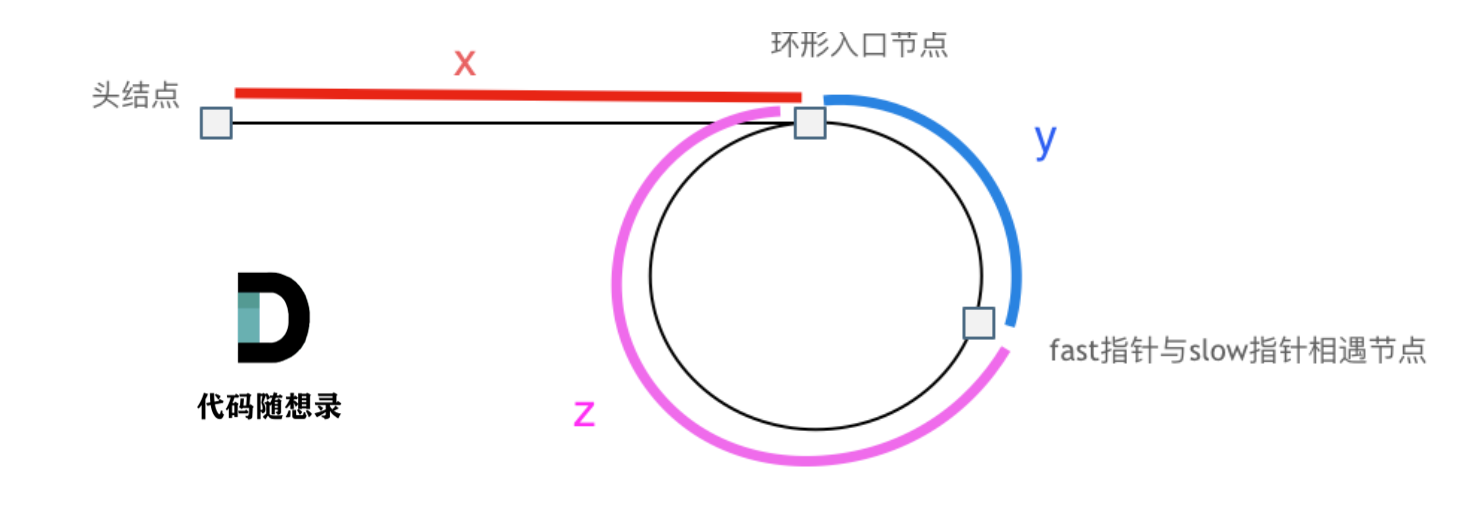
主要流程

快慢指针同时出发，找到在环内的相遇点。

然后分别定义两个指针从head出发和从相遇点出发，二者最终相遇位置为环的入口。

快慢指针

慢指针一次走一下，快指针一次走来两步。

进入环内后，相对于慢指针来说，快指针在以每次走一格的速度接近他，所以早晚有一天会相遇。

在追上慢指针之前，快指针最少在环内已经走了一圈。

数学证明:

代码随想录-环形链表

把环形链表讲清楚！如何判断环形链表？如何找到环形链表的入口？ LeetCode：142.环形链表II

其实我觉得这里的数学证明看看就差不多了，没必要也没啥可总结的了，所以标记下可以学习的地方，笔记上一带而过。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
        while(fast && fast->next){
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow){
                ListNaode* index1 = fast;
                ListNode* index2 = head;
                while(index1 != index2){
                    index1 = index1->next;
                    index2 = index2->next;
                }
                return index1;
            }
        }
        return NULL;
    }
};

目录CONTENT

【代码随想录】二刷-链表

链表

前言

203. 移除链表元素

707.设计链表

206.反转链表

24. 两两交换链表中的节点

19. 删除链表的倒数第 N 个结点

面试题 02.07. 链表相交

142. 环形链表 II

评论区